 DR.S.ARAVAMUDHAN http://www.ugc-inno-nehu.com/ |
 BIODATA CONTACT INFO Curriculum Vitae/Resume webpages_list http://nehuacin.tripod.com Phone Mobile: +919862053872 EMAIL:- inboxnehu_sa@yahoo.com saravamudhan@hotmail.com aram1121944@gmail.com |
For best view,display with: zoom="100%" : text size="smallest" |
Link_1 for Sheets 1 to 10 is HERE on CLICK
Link_2 for Sheets 11 to 13 is HERE on CLICK
Link_3 for Sheets 14 & 15 is HERE on CLICK
Link_5 for Sheets 16 & 17 is HERE on CLICK
Link_6 for Sheets 18 to 20 is HERE on CLICK
Link_7 for Sheets 21 to 22 is HERE on CLICK
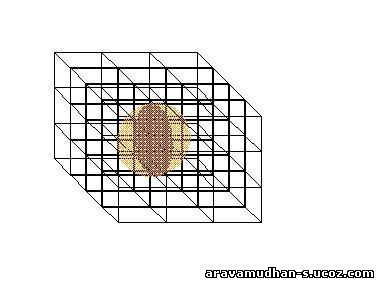
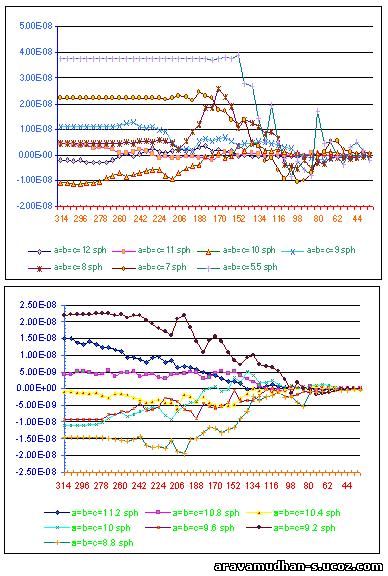
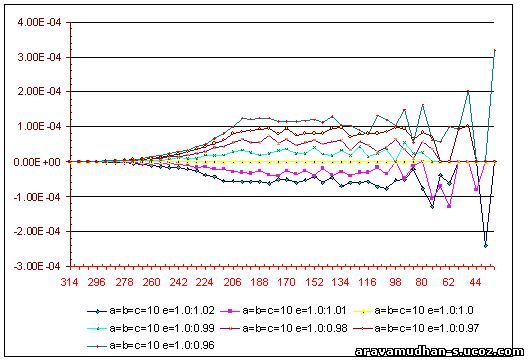
In the following Graphical Plots results of the Calculation of Induced Field Contributions are displayed. A comparison can be made by varying the parametrs for CUBIC Lattice.The inner spherical semimicro Volume Element is varied in radius in steps of 6 Units( as it appears in the X-Axis, the values start with 44/50 and the final value on the left-most is 314 Units) The variations of Lattice parametrs are made to be around the mean value of 10. The variations with small changes in lattice parameter as well as for larger changes are depicted.
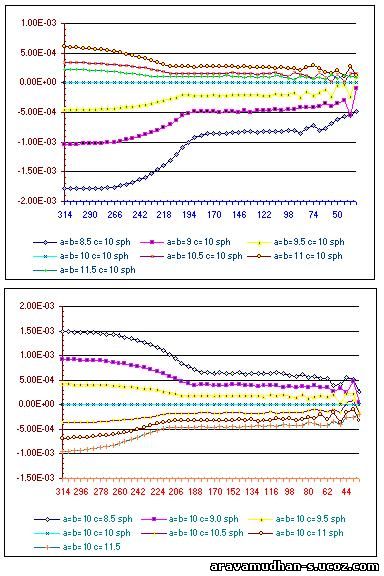
Then similar varitions in lattice parametrs are made for the NON_CUBIC case:: for example,a=b;c by varying a & bfor a=b maintaing a constant value for c. Then a & b are kept constant for a=b varying the value for c.
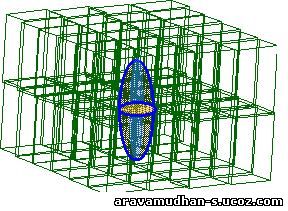
The case of using ellipsoidal semimicro volume element replcing the sphere is also considered. the Ellipsoid of revolution is defined with parameters 'e'.The ellipsoid is specified by one longitudinal axis value bearing a definite ratio to the two equal equitorial axis lengths.
The relevance of the materials presented in the poster can be located in the Book by CHARLES KITTEL entitled:'Introduction to Solid State Physics' in the Chapter-12 on "Dielectric Properties" :'Local Electric Field at an Atom'. In the section on 'Field of Dipoles Inside Cavity' the book contains basic equation and the possile computer algorithm. The case of Spherical Symmetry or Cubic surrounding is explained as the simplest case.
